Computational Methods

In this project, parallel-in-time integration methods are considered as means to reduce the time-to-solution for numerical algorithms concerned with the solution of time-dependent partial differential equations (PDEs) arising in the field of fluid-structure interaction (FSI) modeling. Parallel-in-time integration methods introduce parallelism in the temporal domain and complement parallelization techniques that are applied to the spatial domain, such as domain decomposition methods. This significantly increases the potential for parallel speedup by employing modern computer architectures, ranging from small-scale clusters to massively parallel high-performance computing platforms. Here, the multigrid-reduction-in-time (MGRIT) algorithm is considered as a true multilevel method that can exhibit optimal scaling. MGRIT is based on multigrid reduction and takes inspiration from well-established spatial multigrid methods.

Topics covered within this research area:

• Convergence of MGRIT for the solution of linear and nonlinear (systems of) PDEs: from single- to multiphysics applications relevant to FSI problems in two and three dimensions.
• Derivation of a multilevel convergence framework that generalizes and extends previous two-level theory for linear PDEs.
• Application of the convergence framework is applied to a number of test problems relevant to FSI modeling: solving time-dependent linear PDEs, such as the anisotropic diffusion equation, the wave equation, the linear elasticity equation and the Stokes equation.
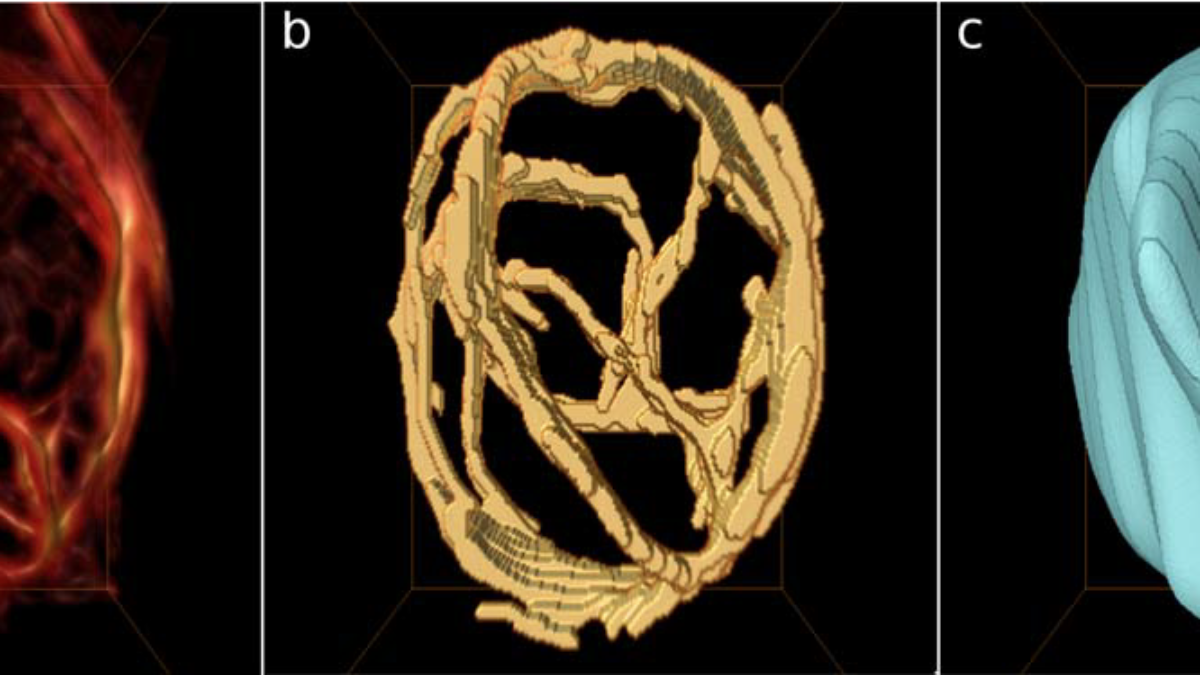
• Time periodic MGRIT variant that can be used in many biomedical engineering applications, e.g., cyclic blood flow in the human heart. 

Biomechanical systems are typically complex, and it is often extremely challenging to establish a univocal relationship between observed biomechanical data and the function of the system. We tackle this challenge by combining methods from machine learning and biomechanical simulations. Particular applications are:

• Relating the structure and function of protein networks [Asgharzadeh et al. 2020a]
• Predicting the age and thus the health of bones [Asgharzahdeh at al. 2020b]

Modelling the musculoskeletal system using a continuum-mechanical approach based on the theory of finite hyperelasticity, together with fine finite element discretisations is not only a challenging, but also a computationally expensive task. Especially in the many query context, which for example can arise when patient specific data is needed, or if parameter studies for healthy and pathological conditions shall be conducted, the simulations become prohibitively expensive or even unfeasible. For this reason, one needs to find ways to reduce the computational costs and this is where the mathematical field of model order reduction (MOR) suggests itself.

One possibility of reducing the computational effort of simulating a high dimensional system of differential equations, in the context of MOR referred to as full order model (FOM), is the projection based MOR. Essentially, this approach aims at reducing the number of degrees of freedom of the system by projecting it onto a lower dimensional subspace of the original high dimensional solution space. That way, a reduced order model (ROM) of lower dimension is obtained. For the determination of a suitable low dimensional subspace, the proper orthogonal decomposition (POD) is a well established and widely applied method. The idea of the POD is based on a split of necessary computations into an offline and an online phase. Therein, it is assumed, that during the offline phase, time and resources are unlimited, i.e. computations involving high dimensional operations can be executed, while aiming at computing only operations of low dimensional complexity during the online phase.

The challenge of constructing a fast and stable skeletal muscle model lies in considering and preserving the structural properties of the FOM when trying to set up a suitable method to obtain the ROM. Properties we focus on are

• dynamics
• incompressibility
• nonlinearity

which means we obtain a nonlinear differential algebraic equation system (DAE) with three fields to be solved for and a saddle point problem in the linear solve.